Weighted Average Tutorial
The concept of a weighted average, a basic average, and how to use our weighted average calculator is covered in this article as well as the embedded video below.
What is an Average?
The average of a group of numbers is simply defined as the sum of the numbers divided by the total amount of numbers. This definition yields a number that when multiplied by the amount of numbers is equal to the sum of the numbers. This number is known as the average and is illustrated in the example below:
Example:
Numbers: 2, 4, 6 (3 numbers in total)
The average = (2 + 4 + 6) / 3 = 12 /3 = 4
Re-arranging the above equation we get: 3*4 = 12, which shows that the average is simply the number that if all the numbers were equal to it would have the same sum as the initial group of numbers.
What is a Weighted Average?
A weighted average is the same as an average except that each number is scaled by importance. This simply means that each number has an associated weight or worth and its importance is calculated by multiplying the number by its weight. The weighted average is calculated as the sum of all the numbers multiplied by their weights divided by the sum of the weights. As shown in the following example, it turns out that an average is simply a weighted average except all the numbers have the same weights. And similar to the average, this definition yields a number that when multiplied by the sum of the weights is equal to the sum of all the numbers multiplied by their weights. The following example better illustrates the above definition of a weighted average:
Example:
| Number | Weight |
|---|---|
| 2 | 6 |
| 4 | 4 |
| 6 | 2 |
The weighted average = (2*6 + 4*4 + 6*2) / (6 + 4 + 2) = 40/12 = 10/3 = 3.3333...
If we assume that the weights in the above example were all the same, W, then the weighted average is simply the average:
| Number | Weight |
|---|---|
| 2 | W |
| 4 | W |
| 6 | W |
The weighted average = (2*W + 4*W + 6*W) / (W + W + W) = (2 + 4 + 6)*W / (3*W) = (2 + 4 + 6) / 3 = 12/3 = 4
Notice how the weights all cancel in the above equation because they are all he same, thus yielding simply the average value. This means that for calculating the average, the weight of the numbers don’t matter and when using our calculator to calculate the average, you can simply input the same number for the weights as shown in the example below.
Example using our Weighted Average Calculator

In the above example, the calculations behind our weighted average calculator are identical with those shown in the previous examples. The calculations for this example are shown below:
Weighted Average = (90*3 + 75*5 + 60*8) / (3 + 5 + 8) = 70.31%
To obtain just the average using our calculator, we can simply input the weight of each course to be the same, for instance choosing the number 1:
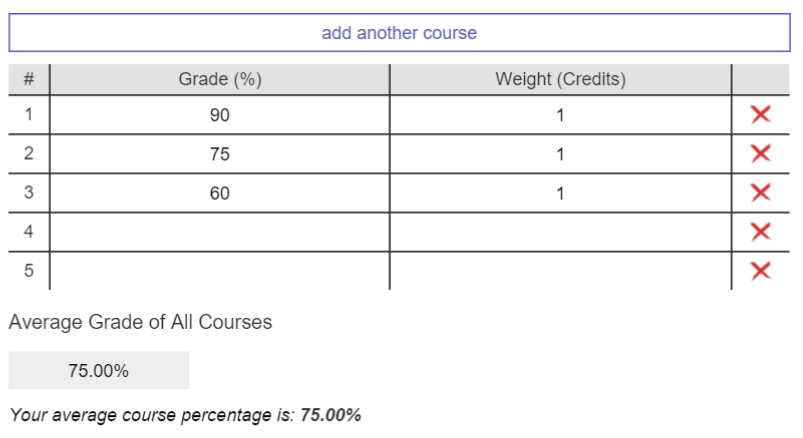
Once again, like in the previous examples above, if the weights of all the numbers are the same then the weighted average and average are the same:
Weighted Average = (90*1+ 75*1 + 60*1)/(3) = (90 + 75 + 60) /3 = Average = 75%
